|

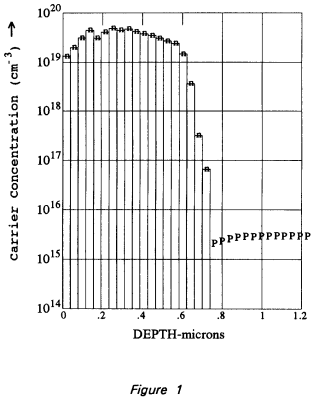
At the bottom right of our spreading resistance reports, we sometimes print some cryptic information. The following is an attempt to explain what it means. We will use the profile in Figure 1 as our example. In this case, we wrote:
1-N Dose = 1.9 x 1015 cm-2 | Sheet = 35 ohms/sq |
Four-point probe sheet = 32 | |
We shall attempt to explain each line. "1-N" denotes the 1st layer and it's type "N". We count the layers from left to right. Sometimes you will see several layers listed so this helps identify which layer the data refers to.
DOSE
"Dose" refers to the dose calculated from the n layer of the spreading resistance profile. We break up the n layer into 19 sub-layers (the number of measurements made within the n layer.) We approximate the dose (net charges per area) of the sub-layer by assuming that the sub-layer has a thickness equal to the depth increment and is of uniform concentration. We then sum the calculated doses from each sub-layer to get the total dose. In this example, concentrations within the n-layer were determined to be:
DEPTH (um) | CONC (cm-3) | | DEPTH (um) | CONC (cm-3) |
.020 | 1.22 x 1019 | | .409 | 3.48 x 1019 |
.058 | 1.83 x 1019 | | .449 | 3.22 x 1019 |
.098 | 2.86 x 1019 | | .487 | 2.82 x 1019 |
.137 | 4.09 x 1019 | | .526 | 2.47 x 1019 |
.175 | 2.85 x 1019 | | .566 | 2.21 x 1019 |
.214 | 3.75 x 1019 | | .605 | 1.35 x 1019 |
.254 | 4.49 x 1019 | | .643 | 3.30 x 1018 |
.292 | 4.13 x 1019 | | .682 | 2.95 x 1017 |
.332 | 4.38 x 1019 | | .722 | 6.04 x 1016 |
.370 | 3.84 x 1019 | | |
The dose of a sub-layer is then the concentration times the thickness (depth increment) which for this profile is 0.0391um or 3.91 x 10-6 cm. (1um = 10-4 cm)
So, the dose of the first sub-layer is approximated as:
1.22 x 1019 cm-3 x 3.91 x 10-6 cm = 4.77 x 1013 cm-2
And the dose of the second sub-layer is:
1.83 x 1019 cm-3 x 3.91 x cm-6 cm = 7.155 x 1013 cm-2
Okay, so we just do this calculation for all the sub-layers and sum them for the total dose.
CONC(cm-3) | Conc. (cm-3) x depth increment (cm) |
1.22 x 1019 | 4.77020 x 1013 cm-2 |
1.83 x 1019 | 7.15530 x 1013 cm-2 |
2.86 x 1019 | 1.11826 x 1014 cm-2 |
4.09 x 1019 | 1.59919 x 1014 cm-2 |
2.85 x 1019 | 1.11435 x 1014 cm-2 |
3.75 x 1019 | 1.46625 x 1014 cm-2 |
4.49 x 1019 | 1.75559 x 1014 cm-2 |
4.13 x 1019 | 1.61483 x 1014 cm-2 |
4.38 x 1019 | 1.71258 x 1014 cm-2 |
3.84 x 1019 | 1.50144 x 1014 cm-2 |
3.48 x 1019 | 1.36068 x 1014 cm-2 |
3.22 x 1019 | 1.25902 x 1014 cm-2 |
2.82 x 1019 | 1.10262 x 1014 cm-2 |
2.47 x 1019 | 9.65770 x 1013 cm-2 |
2.21 x 1019 | 8.64110 x 1013 cm-2 |
1.35 x 1019 | 5.27850 x 1013 cm-2 |
3.30 x 1018 | 1.29030 x 1013 cm-2 |
2.95 x 1017 | 1.15345 x 1012 cm-2 |
6.04 x 1016 | 2.36164 x 1011 cm-2 |
T0TAL DOSE | 1.92980 x 1015 cm-2 |
SHEET
The calculation of the sheet resistance follows the same scheme as the dose except for a few twists. If you have resistors in parallel (Figure 2) the reciprocal of equivalent resistance is equal to the sum of the reciprocal of the resistance of each parallel leg.
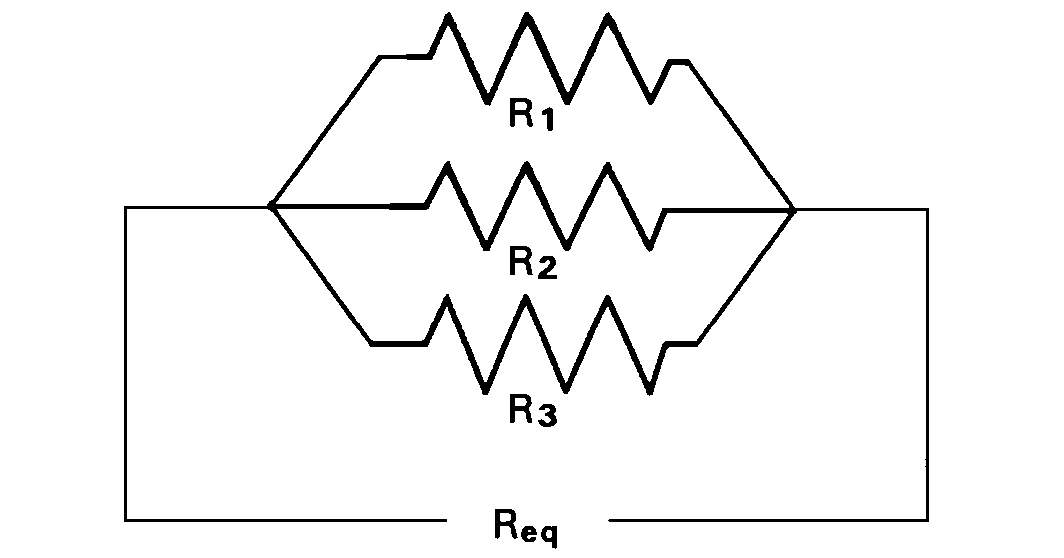
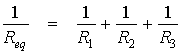
Figure 2
If the resistors were squares of material connected in parallel, the relationship would remain the same:
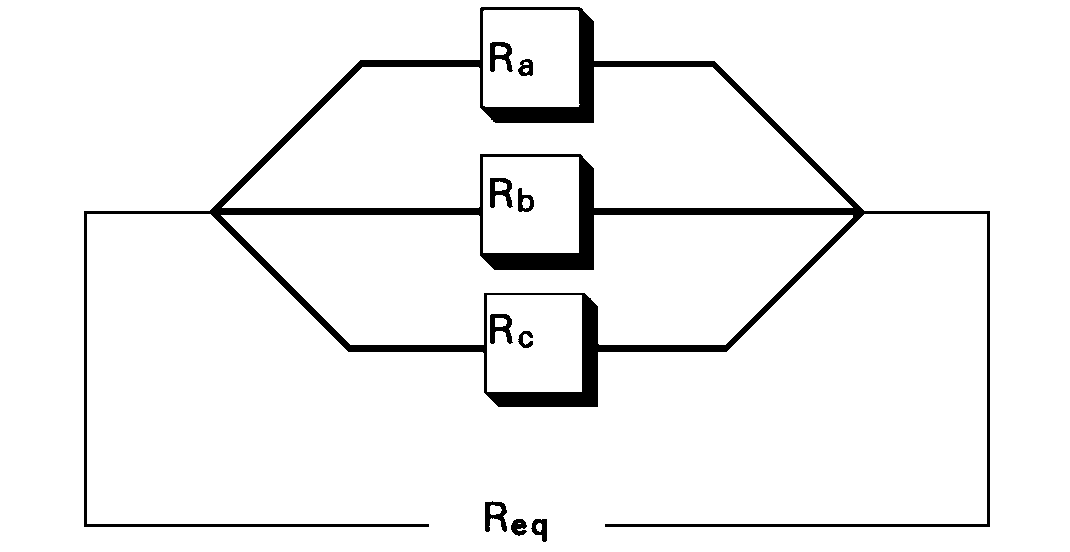
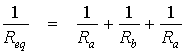
Figure 3
Squares have a convenient electrical property - the resistance encountered between opposite sides is the same for a given material regardless of the size of the square. Because of this we talk of sheet resistance, 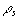 ,in units of "ohms per square". We can then substitute ,in units of "ohms per square". We can then substitute 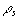 for R in the above equation and we have: for R in the above equation and we have:
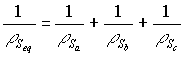
In the case of a "sheet" of uniform resistivity, the sheet resistance 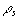 is equal to the bulk resistivity divided by the thickness: is equal to the bulk resistivity divided by the thickness:
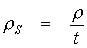
Let's approximate the sheet resistance of each sub layer as the resistivity determined by spreading resistance divided by the depth increment. In our example, the depth increment is 3.91 x 10-6 cm. In the table below, we have used the resistivity associated with each point and divided it by the depth increment to calculate a sheet resistance for each sub-layer. We then calculated the reciprocal of each sheet resistance and added them together. Then we calculated the reciprocal of the total to get the sheet resistance for the n-layer. (Note that we could have introduced the idea of sheet conductance and avoided much of this talk of reciprocals, and we would have arrived at exactly the same result.)
Determined by SRA | Calculated from SRA data |
Depth | 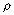 (ohm-cm) (ohm-cm)
| 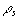 = = 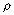 /3.91 x 10-6 cm /3.91 x 10-6 cm
| 1/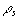 |
.020 | .00507 | 1296.675 ohms/sq | 7.712 x 10-4 |
.058 | .00362 | 925.831 | 1.080 x 10-3 |
.098 | .00239 | 611.253 | 1.635 x 10-3 |
.137 | .00169 | 432.225 | 2.314 x 10-3 |
.175 | .00239 | 611.253 | 1.634 x 10-3 |
.214 | .00184 | 470.588 | 2.125 x 10-3 |
.254 | .00154 | 393.862 | 2.539 x 10-3 |
.292 | .00167 | 427.110 | 2.341 x 10-3 |
.332 | .00158 | 404.092 | 2.475 x 10-3 |
.370 | .00179 | 457.800 | 2.184 x 10-3 |
.409 | .00197 | 503.836 | 1.985 x 10-3 |
.449 | .00213 | 544.757 | 1.836 x 10-3 |
.487 | .00241 | 616.368 | 1.622 x 10-3 |
.526 | .00275 | 703.325 | 1.422 x 10-3 |
.566 | .00304 | 777.494 | 1.286 x 10-3 |
.605 | .00466 | 1191.816 | 8.391 x 10-4 |
.643 | .0117 | 2992.327 | 3.342 x 10-4 |
.682 | .043 | 10997.44 | 9.093 x 10-5 |
.722 | .12 | 30690.54 | 3.258 x 10-5 |
Total 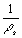 (or (or 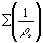 ) ) | 2.855 x 10-2 |
Sheet = 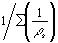 | 35.2 ohms/sq | |
FOUR POINT PROBE SHEET
Finally, "Four-point probe sheet" (4PP) refers to the sheet resistance that we measured on our four-point probe. (You had already guessed that, hadn't you?) If the sample is big enough & unpatterned and if there is a junction and if the sheet rho of the top layer isn't too high, we will measure it. If there's room, we will probe at five locations and report the average.
Nearly always, the sheet resistance obtained by the four-point probe is more reliable than that obtained from SRA so this provides you a benchmark for the SRA measurements. If "Sheet" and "4PP" track each other pretty well, then the SRA is more credible.
Best of all, this quick and dirty "4PP" is free. If you would like something a little more elegant, we will be happy to provide you a 120 point four-point contour map for a little money.
If you have read this technical note in its entirety, we would like to thank you. You paid us a real compliment by bearing through it. And, as always, if you want more information, please let us know.
|